Base cinque: appunti di matematica ricreativa
un singolare anagramma |
società di mercato ... |
... cometa di sorcietà |
Esercitazione con esplorHTML |
Prova le seguenti stringhe di codice html |
1) valutatore con doppio clic sull'area di output : |
| 1bis) come sopra con una piccola differenza ( quale? ) : ******************************************************************** <input id=input type=text value=""> = <input id=output type=text value="" ondblclick="output.value=eval(input.value)"> ******************************************************************** |
| 2) valutatore con singolo clic sul pulsante " = " ( l'evento che attiva la valutazione sarà il clic sul pulsante "=" ) ******************************************************************** <input id=input type=text value="" > <input type=button value="=" onclick="output.value=eval(input.value)" > <input id=output type=text value="" > ******************************************************************** |
con le caselle ottenute da 1 e da 2 valuta le seguenti espressioni: |
| 3) trasformatore in maiuscolo ******************************************************************** <input id=input type=text value="" onkeyup="output.value=input.value.toUpperCase()" > --> <input id=output type=text value="" > ******************************************************************** |
| 4) invertitore di stringhe ******************************************************************** <input id=input type=text value="" onkeyup="output.value=input.value.charAt(input.value.length-1)+ output.value" > --> <input id=output type=text value="" > ******************************************************************** |
da oggi un nuovo blog sulle novità editoriali riguardanti la matematica (e non solo)
| ... il metodo piu' rigoroso e' anche il piu' semplice ed il piu' facile a capirsi. La ricerca del rigore ci conduce a scoprire ragionamenti sempre piu' semplici, e ci apre inoltre la strada a metodi piu' fecondi di quelli antichi, che erano meno rigorosi. |
moltiplicazione con coefficiente intero |
nella seguente clicca ripetutamene sul pulsante Step ( per tornare all'inizio clicca invece sul pulsante Clear ) |
invece di Step si può cliccare sulla figura (solo una prima volta per selezionarla) e premere la barra spaziatrice più volte |
puoi ingrandire o rimpicciolire tutta la figura con i tasti + e - |
notiamo che nb è costruito da b tramite l'addizione così come n è costruito da 1 con l'addizione ( "nb sta a b come n sta 1" ) |
in maniera diversa possiamo dire: nb è la somma di n copie di b (ossia è il risultato del sommare b a se stesso n volte) |
mentre n cresce descrivendo i numeri naturali, m = -n decresce descrivendo gli interi negativi ( dopo la partenza da 0 ) |
| anche per mb = (-n)b possiamo dire che come m è costruito da 1 tramite addizione e opposizione, così mb è ottenuto da b |
| infatti, possiamo prima passare da 1 a -1 (con l'opposizione) e poi sommare tanti -1 fino ad arrivare a -n ; questo porta a costruire, partendo da b, prima -b e quindi n(-b), che coincide con -nb |
| alternativamente, possiamo partire dal sommare tante volte 1 fino ad arrivare a n e poi con l'opposizione passare a -n ; questo altro procedimento porta a costruire mb sommando n volte b per arrivare a nb e poi passando all'opposto -nb |
| in entrambi i casi giungiamo a definire : (-n)b := - nb |
| l'espressione xb (nel nostro caso x=n o x=-n) è detta "prodotto di x per b" ; x è detto "moltiplicatore" o "coefficiente", mentre b è detto "moltiplicando" (ossia : cosa da moltiplicare) |
| "moltiplicazione" è invece l'operazione che porta dalla coppia (moltiplicatore , moltiplicando) al prodotto |
| Conclusione : moltiplicare un moltiplicatore per un moltiplicando significa determinare un prodotto ottenuto a partire dal moltiplicando con lo stesso processo con cui si costruisce il moltiplicatore a partire dall'unità usando addizione ed eventualmente opposizione |
moltiplicazione con coefficiente frazionario |
nella seguente clicca ripetutamene sul pulsante Step |
| 1/n è costruito partendo da 1 in modo che n volte 1/n dia 1, così (1/n)b è costruito da b in modo che n volte (1/n)b dia b, quindi (1/n)b è quel numero x tale che nx=b ( e tale x si indica con b/n ) |
-1/n è costruito partendo da 1 in modo che n volte -1/n dia -1 , così (-1/n)b è costruito da b in modo che n volte (-1/n)b dia -b , quindi (-1/n)b è quel numero x tale che nx=-b ( e tale x è (-b)/n = -b/n ) |
| notiamo che anche nei due precedenti punti si sono utilizzate solo l'addizione e l'opposizione (ossia la simmetria rispetto allo zero) |
| se m è un numero intero positivo, m/n è costruito a partire da 1 sommando m volte quel numero che sommato n volte dà 1, così (m/n)b è costruito da b sommando m volte quel numero che sommato n volte dà b, quindi (m/n)b = m(b/n) |
se m è un numero intero positivo, -m/n è costruito a partire da 1 sommando m volte quel numero che sommato n volte dà -1 , così (-m/n)b è costruito da b sommando m volte quel numero che sommato n volte dà -b, quindi (-m/n)b=m(-b/n)=-m(b/n)=-(m/n)b |
| anche negli ultimi casi sono usate solo addizione e opposizione |
nella seguente scegli prima g e poi usa il pulsante Step ( il valore di n è anche riportato nello stesso pulsante Step) |
per la moltiplicazione con coefficiente complesso vedi il post del 07/12/2003 |
la funzione esponenziale naturale ( vedi anche questo documento )
( avendo MathView o LiveMath è possibile scaricare il corrispondente
foglio di lavoro interattivo )
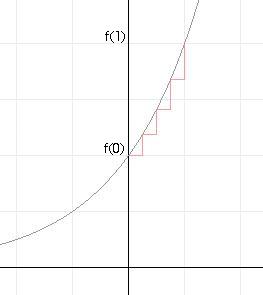
| Nella figura che si apre cliccando sul pulsante qui accanto è dato il grafico della legge di crescita composta |
|
| L'esempio tipico di tale crescita è la capitalizzazione composta. I parametri sono i seguenti: h è il tasso iniziale di crescita, f è la lunghezza del periodo di capitalizzazione. La variabile sull'asse delle ascisse è il tempo. Il capitale iniziale (x=0) è unitario. La formula di tale legge è : ( 1 + h f )x/f . | |
| Lasciando il tasso pari a 1 e facendo tendere f a 0 si ha la capitalizzazione continua al tasso 1 la cui legge è y=exp(x) e che vale e (numero di Nepero) per x=1. Muovi con il mouse il punto d verso l'asse verticale ( facendo così tendere f a 0 ) . | |
| g è il numero di periodi di capitalizzazione da considerare: posto f > 0 (come naturale), in ogni periodo è mostrato da un segmento orizzontale il valore del capitale congelato a inizio periodo; si ha così un'approssimazione a scala di un tratto del grafico della legge. | |
| In forma di potenza la funzione exp(x) coincide con ex . Il punto n è ( 1 , e ) . | |
| la "geometry applet" | |
| scaricabile da questa pagina web | |
| muovi i punti colorati della seguente figura | il codice che genera questa applet è il seguente |
<applet codebase=" http://aleph0.clarku.edu/~djoyce/java/Geometry/"code="Geometry" height="380" width="320" archive="Geometry.zip"> <param name="background" value="35,19,100"> <param name="title" value="I.47"> <param name="e[1]" value="B;point;free;100,200"> <param name="e[2]" value="C;point;free;230,200"> <param name="e[3]" value="O;point;midpoint;B,C;none;none"> <param name="e[4]" value="OABC;circle;radius;O,B;none;none;none;none"> <param name="e[5]" value="A;point;circleSlider;OABC,140,100"> <param name="e[6]" value="ABC;polygon;triangle;A,B,C;none;none;black;random"> <param name="e[7]" value="A2;polygon;square;C,B;none;none;black"> <param name="e[8]" value="B2;polygon;square;B,A;none;none;black"> <param name="e[9]" value="C2;polygon;square;A,C;none;none;black"> <param name="e[10]" value="G;point;vertex;B2,3"> <param name="e[11]" value="F;point;vertex;B2,4"> <param name="e[12]" value="K;point;vertex;C2,3"> <param name="e[13]" value="H;point;vertex;C2,4"> <param name="e[14]" value="D;point;vertex;A2,3"> <param name="e[15]" value="E;point;vertex;A2,4"> <param name="e[16]" value="AL;line;foot;A,D,E"> <param name="e[17]" value="L;point;last;AL"> <param name="e[18]" value="J;point;intersection;B,C,A,L;0;green"> <param name="pivot" value="J"> <param name="e[19]" value="AD;line;connect;A,D"> <param name="e[20]" value="CF;line;connect;C,F"> <param name="e[21]" value="BK;line;connect;B,K"> <param name="e[22]" value="AE;line;connect;A,E"> </applet> | |
Come si vede dal codice qui a destra, l'applet è gestita dal file geometry.zip e dai parametri, la cui scelta produce la figura direttamente dal codice html della pagina, a differenza di cabrijava, che richiede la presenza sul server non solo di un file di classi java, ma anche di una figura di cabri, diversa da caso a caso. Pertanto questo tipo di applet è più economico in termini di files che devono essere presenti sul web per le visualizzazioni geometriche e si avvicina a PGC (plane graphic calculator, ma anche "piano grafico complesso") per la sua filosofia di utilizzo, pur con impostazione geometrica di tipo diverso. | |
nel piano ( usando i numeri complessi ) |
| funzioni elementari | |
| ( muovi il punto a nelle figure ) | |
| costanti | |
| proporzionalita' dirette | |
| proporzionalita' inverse | |
| potenze | |
| esponenziali | |
| sinusoidi | |
| cosinusoidi | |
| tangentoidi | |
a l c u n i c o l l e g a m e n t i i n t e r e s s a n t i | |
| numeri razionali e algebra elementare | http://www.iprase.tn.it/servizi/poli/matematica/numeri_razionali.pdf |
| Excel | http://www.denicolaonline.it/corsionline/excel/excel.htm |
| derivate | http://www.denicolaonline.it/corsionline/teoder.htm http://members.xoom.virgilio.it/luckydb/derivate2000/teoria.html |
| dispense di matematica varia | http://www.elettronica.ingegneria.unige.it/Laurea_3_anni/Dispense/ http://www.robertobigoni.it/frames.htm http://www.dipmat.unipg.it/~candelor/didattica.htm |
| precorsi per l'università | http://www.dipmat.unipg.it/didattica/clmat/AA2003-04/dispense_precorsi.pdf |
| serie di Fourier e altro | http://mathsun1.univ.trieste.it/~tironi/Fouriercorr.pdf http://www.ateneonline.it/delcorso/link.asp http://digilander.libero.it/eric5/fourier.html ( vedi anche: http://digilander.libero.it/eric5/software.html ) |
| traslazioni , rotodilatazioni ... | |
| ... e loro traiettorie ( clicca sui pulsanti ) | |
| ( muovi b e z = a , c , d nelle figure ) | |
| traslazione di "vettore" b Tb : z --> Tb ( z ) := z + b | |
| rotodilatazione di "flettore" b Rb : z --> Rb ( z ) := z · b | |
l o g a r i t m i : proprietà ( regole di calcolo ) fondamentali | |
Partiamo da: y = ax | |
y = expa ( x ) ( definizione di exp ) | x = loga ( y ) ( definizione di log ) |
y' = expa ( x' ) | x' = loga ( y' ) |
| y · y' = expa ( x ) · expa ( x' ) | x + x' = loga ( y ) + loga ( y' ) |
a x + x' = a x · a x' ( proprietà della somma degli esponenti ) | |
y · y' = ax · ax' = ax+x' = expa ( x + x' ) | => x + x' = loga ( y · y' ) |
| expa ( x + x' ) = expa ( x ) · expa ( x' ) | loga ( y ) + loga ( y' ) = loga ( y · y' ) |
(1) regola del logaritmo di un prodotto : loga ( y · y' ) = loga ( y ) + loga ( y' ) | |
a x x' = ( a x ) x' ( proprietà del prodotto degli esponenti ) | |
y = expa ( x ) | x = loga ( y ) |
yc = ( expa(x) )c = ( ax )c = ax·c = expa(x·c) | => x c = loga ( y c ) |
| expa ( x · c ) = ( expa (x) ) c | loga (y) · c = loga ( y c ) |
(2) regola del logaritmo di una potenza : loga ( y c ) = c · loga (y) | |
| c = -1 | b = y c ( => c = logy (b) ) |
| loga ( y -1 ) = (-1) · loga (y) | loga (y c) = loga (y) · c = loga (y) · logy (b) |
| loga ( 1 / y ) = - loga ( y ) | loga ( b ) = loga (y) · logy (b) |
loga( z / y )=loga(z · 1/y)=loga(z) - loga(y) | logy ( b ) = loga ( b ) / loga ( y ) |
| ^ regola del logaritmo di un quoziente | ^ regola del cambiamento di base |
classe 4^S
1) Sia f(x) = -1/x a) determinare la crescita di f nel passaggio della variabile indipendente da x a x+Dx , ossia Df(x) b) determinare la velocità di crescita di f nel passaggio della variabile indipendente da x a x+Dx c) determinare la velocità di crescita di f istantanea nel valore x della variabile indipendente |
2) Supponendo che una funzione f abbia la seguente proprietà: f( x + Dx ) - f( x ) = f( x' + Dx ) - f(x') per ogni scelta di x, x', Dx a) provare che: f(x+1) - f(x) = f(1) - f(0) per ogni scelta di x b) provare che: f(x + 1/4) - f(x) = f(1/4) - f(0) per ogni scelta di x c) provare che: 4(f(1/4)-f(0))=f(1)-f(0) e quindi f(1/4) - f(0) = (f(1) - f(0))/4 d) provare che: f(3/4)=f0)+(3/4)(f(1)-f(0)) . e) Qual è la espressione generale di f(m/n) se f(0)=3 e f(1)=5 ? f) Disegnare il grafico di f nel caso in cui si abbia f(0)=3 e f(1)=5 . |
3) Supponendo che una funzione f abbia la seguente proprietà: f( x + Dx )/f( x )=f(x'+ Dx)/f(x') per ogni scelta di x, x', Dx a) provare che: f(x+1)/f(x) = f(1)/f(0) per ogni scelta di x b) provare che: f(x+1/4)/f(x)=f(1/4)/f(0) per ogni scelta di x c) provare che: ( f(1/4) / f(0) )4 = f(1) / f(0) e quindi f(1/4) / f(0) = ( f(1) / f(0) )1/4 d) provare che: f ( 3/4 ) = f(0) ( f(1) / f(0) )3/4 . e) Qual è la espressione generale di f(m/n) se f(0)=2 e f(1)=4 ? f) Disegnare il grafico di f nel caso in cui si abbia f(0)=2 e f(1)=4. |
4) Considerando un capitale pari a 1000 euro e prendendo come unità di tempo l'anno, qual è l'espressione matematica che dà il valore del capitale a fine anno nel caso si applichi un tasso di interesse pari a 0.01 (ossia 1%) e si ricapitalizzi a ogni fine mese (quindi 12 volte) ? |
| funzione incrementale g associata a una funzione f e a un valore x dell'argomento ; operatore D |
| g è definita dalla formula g(p)=f(x+p)-f(x) ; in genere g(p) dipende da x oltre che dall'incremento p, ossia g(p) è funzione dell'incremento, ma la funzione g stessa varia al variare della scelta di x |
| nella seguente agendo su d si modifica x e agendo su c si modifica p; il punto g descrive il grafico della funzione incrementale di f con valore x dell'argomento; come si vede, la funzione g cambia al variare di x |
| Nell'espressione f(x+p)-f(x) sono presenti le due variabili x e p, entrambe variabili indipendenti e che variano indipendentemente l'una dall'altra; la variabile p è l'incremento della x (nel passaggio da x a x+p) e viene usualmente indicato con il simbolo Dx (in cui la lettera "delta" ricorda la lettera "d" di "differenza"); pertanto x e Dx sono entrambe variabili indipendenti. D è detto "operatore differenza" . |
| Dx, che è detta "variabile incrementale della variabile x", è indipendente dalla variabile x. |
| La espressione f(x) è una variabile dipendente dalla variabile x, mentre l'espressione f(x+Dx)-f(x) è una variabile dipendente dalle due variabili x e Dx. |
| dal momento che Dx è l'incremento della variabile dipendente f(x) nel passaggio della x al valore x+Dx , si pone: Df(x) = f(x+Dx)-f(x) |
| l'espressione Df(x) deve essere interpretata come D( f(x) ) , ossia il simbolo D agisce sull'espressione f(x) (contenente la sola variabile x) per produrre una nuova espressione contenente sia la variabile x sia la corrispondente variabile incrementale Dx (e per tale motivo Df(x) è detta "espressione incrementale nella variabile x" ). Ad esempio: D( x2 ) = (x + Dx)2 - x2 = 2xDx + (Dx)2 . |
| nell'espressione f(x) la f (da sola) indica la funzione, mentre l'espressione f(x) è detta "espressione funzionale nella variabile x" o anche "forma funzionale nella variabile x". Potremmo applicare la stessa funzione f ad un'altra variabile, ad esempio t, e ottenere l'espressione funzionale f(t) nella variabile t. Sarebbe bene distinguere sempre fra "funzione" ed "espressione funzionale" |
| l'operatore D può essere applicato anche al solo simbolo di funzione f per ottenere una nuova funzione Df , ponendo: (Df)(x)(p) = f(x+p)-f(x) ; ciò significa che ad ogni x la funzione Df associa non un numero, bensì la funzione incrementale g , associata alla f e al valore x dell'argomento di f, che abbiamo detto essere quella che associa a ogni p il valore f(x+p)-f(x) : quindi (Df)(x)=g (e fra l'altro da ciò viene esplicitata la dipendenza di g dallo x scelto). Pertanto (Df)(x) non è un numero, ma un'intera funzione. |
| possiamo riassumere quanto detto ai due punti precedenti con la seguente uguaglianza, che mette in relazione la funzione Df con l'espressione D(f(x)) : (Df)(x)( Dx ) = f(x+Dx)-f(x) = D( f(x) ) |
| ultima osservazione, questa volta di carattere geometrico: la funzione incrementale g = (Df)(x) , associata alla funzione f e al valore x dell'argomento, ha (v. la figura sopra) un grafico ottenuto per traslazione dal grafico della funzione f con la traslazione che porta il punto (x , f(x) ) nell'origine, il che equivale a considerare degli assi ausiliari centrati, invece che nell'origine, nel punto ( x , f(x) ) . |
Spesso gli studenti confondono la proporzionalità diretta con la proprietà di monotonicità (al crescere della variabile indipendente cresce la variabile dipendente) (non pensano ovviamente neanche per un attimo a rette con pendenza negativa). Per contro ( evviva la coerenza ! ) fanno diventare additiva (quindi lineare) praticamente ogni funzione che incontrano negli esercizi (monotòna o non), a cominciare dalla quadratica e dalla radice quadrata. La coerenza, forse, è nell'atteggiamento di "semplificazione a tutti i costi" (compreso - come detto - quello della assenza della "coerenza", già faticosa ricerca, attualmente sempre più diffusamente neanche gadget di distinzione);
per quanto riguarda l'errore sulla proporzionalità, si semplifica qualitativizzando un caso particolare di un enunciato quantitativo (raffazzonamento semantico, tipico della ripetizione mnemonica vagamente collegata a un'idea), mentre nella iper-linearizzazione (direi anzi pan-linearizzazione) si semplifica la formula (raffazzonamento sintattico, tipico dell'identificazione "simboli=gesso sprecato su lavagna", per la serie ... "visto che devo per forza scrivere una formula, buttiamo giù questa!", quindi ripetizione mnemonica per nulla collegata a un'idea).
L'incoerenza: ecco il perché (e si tratta di un "perché" di causa ma anche di comodo fine di manipolabilità sociale) la "matematica" è diventata nella considerazione usuale una malattia del sangue: la ... "mattia ematica".
(in effetti l'insegnante che vuole cercare effettivamente di formare e non solo "informare formalmente" è soggetto a periodi di donchisciottiana (nonché normalissima per qualunque situazione di sforzo e studio non obliterata da delphinizzazioni) "circolazione sanguigna non ottimale", per i quali i più avanzati e labellotropi ("label oriented") manuali italiani di didattica avranno immancabilmente stanato lo ... IETI ( Interchangeable English Terminological Item ) accademicamente e onomatologicamente appropriato)
Una osservazione aggiuntiva sulle funzioni a incrementi proporzionali |
| Dalla proprietà di f(x+p) - f(x) = g(p) di esser costante rispetto alla x ricaviamo una importante proprietà per la funzione degli incrementi g : g(p+p')=f(p+p')-f(0)=f(p+p')-f(p)+f(p)-f(0)=g(p')+g(p)=g(p)+g(p') ossia: la funzione g è "additiva", cioè porta somme in somme. Ciò comporta che g(nx)=ng(x), per ogni n intero positivo, il che a sua volta comporta che: k = g(1)
Una funzione definita sui razionali e additiva è detta anche "funzione lineare di variabile razionale". La funzione g degli incrementi di una funzione f a incrementi proporzionali è un esempio di tale tipo di funzione . *** L'usuale definizione di proporzionalità diretta definisce come tale una funzione g tale che : Tale proprietà comporta, se g è definita su tutti i razionali positivi, che si abbia: pertanto si ha: g(m/n) = m g(1) / n = g(1) m/n Quindi una g definita sui razionali positivi con la proprietà data all'inizio di "estraibilità del coefficiente" (e questa è in effetti la proprietà di "linearità") deve avere equazione : g(x) = g(1) x L'estensione di tale formula anche ai razionali non positivi (quindi allo zero e ai razionali negativi) conduce al tipo di funzione di cui sopra si è trattato. |
| il "decalogo" della moltiplicazione fra numeri complessi |
| Puoi muovere col mouse i numeri complessi a e b. Il prodotto a*b è f . |
| il piano nelle figure può essere traslato col mouse tenendo premuto il tasto CONTROL (Ctrl) |
1) prendiamo in esame l'esempio: 3*b = (1+1+1)*b = b+b+b (ad ogni 1 si sostituisce b) |
| 2) sappiamo che l'ortogonale (antiorario) di z=x+yi è ort(z)=-y+xi, in particolare ort(1) = i |
| 3) procediamo come in 1) con: (3+2i)*b=(1+1+1+ort(1)+ort(1))*b=b+b+b+ort(b)+ort(b) |
| 4) si "induce" la definizione: a*b = (p+qi)*b = p b + q ort(b) = Re(a) b + Im(a) ort(b) |
| 5) se b = x+yi , si ha: a*b = (p+qi)*(x+yi) = p(x+yi) + q(-y+xi) = (px-qy) + (py+qx)i |
| 6) graficamente, moltiplicare a per b significa "rotodilatare" a così come 1 si "rotodilata" in b |
| 7) la "dilatazione" può essere anche "contrazione", a seconda di quanto b "dista" da 0 |
| 8) conj(b)=Re(b)-Im(b)i è il "coniugato" di b ossia il simmetrico di b rispetto all'asse reale |
| 9) b "dista" da 0 quanto 1 da 0 quando la stessa rotodilatazione porta 1 in b e conj(b) in 1 |
| 10) per visualizzare 9) porta a in conj(b); in tal caso, se b dista 1 da 0, f=a*b=conj(b)*b=1 |
| per comodità si è posto a=conj(b), quindi b dista 1 da 0 quando f=conj(b)*b=1 |
| Rotazioni intorno all'origine 0 (angoli) : muovi c per scegliere l'angolo |
| una rotazione a intorno all'origine (angolo) porta 1 in a(1)=(a,b)=f |
| proprietà 1) a( i ) = a( 0 , 1 ) = ( -b , a ) = g (ortogonalità) |
proprietà 2) a( d ) = a( x , y ) = a( x 1 + y i ) = x f + y g = n (conservazione delle coordinate) |
| proprietà 3) a( h ) = a( a , -b ) = 1 (rigidità) |
| (x', y') = a(x,y) = x a(1) + y a(i) = x(a,b) + y(-b,a) = ( xa-yb , xb+ya ) (rotazione) | |
| ( 1 , 0 ) = a( a , -b ) = ( a2 + b2 , 0 ) , quindi a2 + b2 = 1 (relazione pitagorica) | |
cos a := a (definizione di coseno) | sin a := b (definizione di seno) |
G := C1 := { (a,b) : a2 + b2 = 1 } (circonferenza goniometrica) | |
| c = ( p , q ) = t f , f Î G , t ³ 0 Þ t = | c | := Ö( p2 + q2 ) (modulo) | |
| ( 1 , m ) = | ( 1 , m ) | a(1) Þ cos a ¹ 0 , m = tg a := sin a / cos a (tangente) | |
| Se durante il navigare in questo o in altri siti appare una finestra che propone o esige il tuo assenso o una conferma ad una installazione di programma o esorta a dire "sì" o dare "ok" a qualche azione o qualche "perfezione", consiglio è di chiuderla con l' x posta sulla monella in alto a destra o - se tale facoltà non l'han lasciata - beccando la finestra incriminata con clic sulla sua barra superiore e poi schiacciando insieme ALT-F4. Di questo la cagione dove sta? Risponne er cinesino pe' cita' : " Alma a commelcio è pubblicità , mentle suo còlpo è fatto . . . pe' flega' " |
| |
Quale è la figura escheriana (paradossale) ? | |