classe 4^S

 

1) Sia f(x) = -1/x a) determinare la crescita di f nel passaggio della variabile indipendente da x a x+Dx , ossia Df(x) b) determinare la velocità di crescita di f nel passaggio della variabile indipendente da x a x+Dx c) determinare la velocità di crescita di f istantanea nel valore x della variabile indipendente

2) Supponendo che una funzione f abbia la seguente proprietà:           f( x + Dx ) - f( x ) = f( x' + Dx ) - f(x')     per ogni scelta di x, x', Dx a) provare che: f(x+1) - f(x) = f(1) - f(0) per ogni scelta di x b) provare che: f(x + 1/4) - f(x) = f(1/4) - f(0)  per ogni scelta di x c) provare che: 4(f(1/4)-f(0))=f(1)-f(0)          e quindi f(1/4) - f(0) = (f(1) - f(0))/4 d) provare che:  f(3/4)=f0)+(3/4)(f(1)-f(0)) . e) Qual è la espressione generale di f(m/n) se f(0)=3 e f(1)=5 ? f) Disegnare il grafico di f nel caso in cui si abbia f(0)=3 e f(1)=5 .

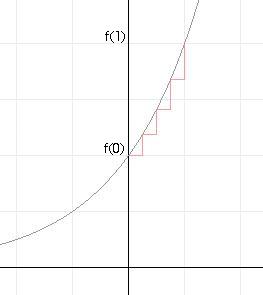
3) Supponendo che una funzione f abbia la seguente proprietà:       f( x + Dx )/f( x )=f(x'+ Dx)/f(x') per ogni scelta di x, x', Dx a) provare che: f(x+1)/f(x) = f(1)/f(0) per ogni scelta di x b) provare che: f(x+1/4)/f(x)=f(1/4)/f(0) per ogni scelta di x c) provare che:    ( f(1/4) / f(0) )4 = f(1) / f(0)                e quindi f(1/4) / f(0) = ( f(1) / f(0) )1/4 d) provare che:    f ( 3/4 ) = f(0) ( f(1) / f(0) )3/4 . e) Qual è la espressione generale di f(m/n) se f(0)=2 e f(1)=4 ? f) Disegnare il grafico di f nel caso in cui si abbia f(0)=2 e f(1)=4.

4) Considerando un capitale pari a 1000 euro e prendendo come unità di tempo l'anno, qual è l'espressione matematica che dà il valore del capitale a fine anno nel caso si applichi un tasso di interesse pari a 0.01 (ossia 1%) e si ricapitalizzi a ogni fine mese (quindi 12 volte) ?

 

da oggi un nuovo blo...

da oggi un nuovo blog sulle novità editoriali riguardanti la matematica (e non solo)

                                      http://mathematedita.splinder.it

... il metodo ...

... il metodo piu' rigoroso e' anche il piu' semplice ed il piu' facile a capirsi. La ricerca del rigore ci conduce a scoprire ragionamenti sempre piu' semplici, e ci apre inoltre la strada a metodi piu' fecondi di quelli antichi, che erano meno rigorosi. David Hilbert

...

 

 

numeri

target=_blank
href="http://w3.romascuola.net/gspes/materiali/numeri/_inizio.html">numeri

dens...

densità, continuità, divisibilità

il teorema di Archimede

 

moltip...

moltiplicazione con coefficiente intero

nella seguente clicca ripetutamene sul pulsante Step ( per tornare all'inizio clicca invece sul pulsante Clear )

invece di Step si può cliccare sulla figura (solo una prima volta per selezionarla) e premere la barra spaziatrice più volte

puoi ingrandire o rimpicciolire tutta la figura con i tasti + e -

notiamo che nb è costruito da b tramite l'addizione così come n è costruito da 1 con l'addizione ( "nb sta a b come n sta 1" )

in maniera diversa possiamo dire: nb è la somma di n copie di b (ossia è il risultato del sommare b a se stesso n volte)

mentre n cresce descrivendo i numeri naturali, m = -n decresce descrivendo gli interi negativi ( dopo la partenza da 0 )

anche per mb = (-n)b possiamo dire che come m è costruito da 1 tramite addizione e opposizione, così mb è ottenuto da b

infatti, possiamo prima passare da 1 a -1 (con l'opposizione) e poi sommare tanti -1 fino ad arrivare a -n ; questo porta a costruire, partendo da b, prima -b e quindi n(-b), che coincide con -nb

alternativamente, possiamo partire dal sommare tante volte 1 fino ad arrivare a n e poi con l'opposizione passare a -n ; questo altro procedimento porta a costruire mb sommando n volte b per arrivare a nb e poi passando all'opposto -nb

in entrambi i casi giungiamo a definire : (-n)b := - nb

l'espressione xb (nel nostro caso x=n o x=-n) è detta "prodotto di x per b" ; x è detto "moltiplicatore" o "coefficiente", mentre b è detto "moltiplicando" (ossia : cosa da moltiplicare)

"moltiplicazione" è invece l'operazione che porta dalla coppia (moltiplicatore , moltiplicando) al prodotto

Conclusione : moltiplicare un moltiplicatore per un moltiplicando significa determinare un prodotto ottenuto a partire dal moltiplicando con lo stesso processo con cui si costruisce il moltiplicatore a partire dall'unità usando addizione ed eventualmente opposizione

moltiplicazione con coefficiente frazionario

nella seguente clicca ripetutamene sul pulsante Step

1/n è costruito partendo da 1 in modo che n volte 1/n dia 1, così (1/n)b è costruito da b in modo che n volte (1/n)b dia b, quindi (1/n)b è quel numero x tale che nx=b ( e tale x si indica con b/n )

-1/n  è costruito partendo da 1 in modo che n volte  -1/n dia -1 , così  (-1/n)b  è costruito da  b  in modo che  n volte  (-1/n)b  dia  -b , quindi (-1/n)b è quel numero x tale che nx=-b ( e tale x è (-b)/n = -b/n )

notiamo che anche nei due precedenti punti si sono utilizzate solo l'addizione e l'opposizione (ossia la simmetria rispetto allo zero)

se m è un numero intero positivo, m/n è costruito a partire da 1 sommando m volte quel numero che sommato n volte dà 1, così (m/n)b è costruito da b sommando m volte quel numero che sommato n volte dà b, quindi (m/n)b = m(b/n)

se m è un numero intero positivo, -m/n è costruito a partire da 1 sommando m volte quel numero che sommato n volte dà -1 , così       (-m/n)b è costruito da b sommando m volte quel numero che sommato n volte dà -b, quindi (-m/n)b=m(-b/n)=-m(b/n)=-(m/n)b

anche negli ultimi casi sono usate solo addizione e opposizione

nella seguente scegli prima g e poi usa il pulsante Step ( il valore di n è anche riportato nello stesso pulsante Step)

per la moltiplicazione con coefficiente complesso vedi il post del 07/12/2003

la funzione esponenz...

la funzione esponenziale naturale ( vedi anche questo documento )

( avendo MathView o LiveMath è possibile scaricare il corrispondente

foglio di lavoro interattivo )

Nella figura che si apre cliccando sul pulsante qui accanto è dato il grafico della legge di crescita composta
L'esempio tipico di tale crescita è la capitalizzazione composta. I parametri sono i seguenti: h è il tasso iniziale di crescita, f è la lunghezza del periodo di capitalizzazione. La variabile sull'asse delle ascisse è il tempo.  Il capitale iniziale (x=0)  è unitario. La formula di tale legge è :     ( 1 + h f )x/f .
Lasciando il tasso pari a 1 e facendo tendere f a 0 si ha la capitalizzazione continua al tasso 1 la cui legge è y=exp(x) e che vale e (numero di Nepero) per x=1. Muovi con il mouse il  punto d verso l'asse verticale  ( facendo così tendere f a 0 ) .
g è il numero di periodi di capitalizzazione da considerare: posto  f > 0 (come naturale), in ogni periodo è mostrato da un segmento orizzontale il valore del capitale congelato a inizio periodo; si ha così un'approssimazione a scala di un tratto del grafico della legge.
In forma di potenza la funzione exp(x) coincide con  ex . Il punto  n  è  ( 1 , e ) .

 

la "geomet...

la "geometry applet"
scaricabile da questa pagina web
muovi i punti colorati della seguente figura	il codice che genera questa applet è il seguente
	<applet codebase="http://aleph0.clarku.edu/~djoyce/java/Geometry/" code="Geometry" height="380" width="320" archive="Geometry.zip"> <param name="background" value="35,19,100"> <param name="title" value="I.47"> <param name="e[1]" value="B;point;free;100,200"> <param name="e[2]" value="C;point;free;230,200"> <param name="e[3]" value="O;point;midpoint;B,C;none;none"> <param name="e[4]" value="OABC;circle;radius;O,B;none;none;none;none"> <param name="e[5]" value="A;point;circleSlider;OABC,140,100"> <param name="e[6]" value="ABC;polygon;triangle;A,B,C;none;none;black;random"> <param name="e[7]" value="A2;polygon;square;C,B;none;none;black"> <param name="e[8]" value="B2;polygon;square;B,A;none;none;black"> <param name="e[9]" value="C2;polygon;square;A,C;none;none;black"> <param name="e[10]" value="G;point;vertex;B2,3"> <param name="e[11]" value="F;point;vertex;B2,4"> <param name="e[12]" value="K;point;vertex;C2,3"> <param name="e[13]" value="H;point;vertex;C2,4"> <param name="e[14]" value="D;point;vertex;A2,3"> <param name="e[15]" value="E;point;vertex;A2,4"> <param name="e[16]" value="AL;line;foot;A,D,E"> <param name="e[17]" value="L;point;last;AL"> <param name="e[18]" value="J;point;intersection;B,C,A,L;0;green"> <param name="pivot" value="J"> <param name="e[19]" value="AD;line;connect;A,D"> <param name="e[20]" value="CF;line;connect;C,F"> <param name="e[21]" value="BK;line;connect;B,K"> <param name="e[22]" value="AE;line;connect;A,E"> </applet>
Come si vede dal codice qui a destra, l'applet è gestita dal file geometry.zip e dai parametri, la cui scelta produce la figura direttamente dal codice html della pagina, a differenza di cabrijava, che richiede la presenza sul server non solo di un file di classi java, ma anche di una figura di cabri, diversa da caso a caso. Pertanto questo tipo di applet è più economico in termini di files che devono essere presenti sul web per le visualizzazioni geometriche e si avvicina a PGC (plane graphic calculator, ma anche "piano grafico complesso") per la sua filosofia di utilizzo, pur con impostazione geometrica di tipo diverso.

...

 

nel piano ( usando i numeri complessi )

assiomi per i numeri...

assiomi per i numeri reali