Ortogonalità e modulo in R³

 

 

approssimazioni di exp(it)

 

 

Base cinque: appunti di matematica ricreativa

 

 

The importance of being ... conjugated

 

l' Informatica come disciplina e come strumento

Una proposta  per la strutturazione dell'insegnamento dell'informatica
 per il curricolo del livello formativo (livello A1 = modulo A1.1 + modulo A1.2)

 

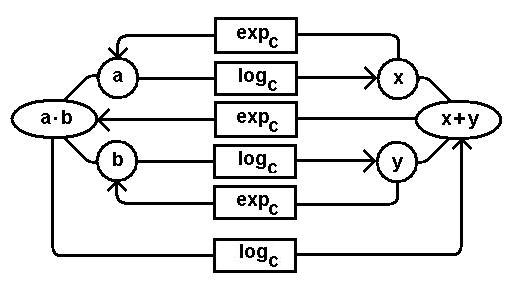
il logaritmo (in base c) del prodotto ab coincide con la somma dei logaritmi dei fattori

 

Una possibile scansione in (macro-)moduli dei contenuti matematici di base di un corso triennale strutturato in tre livelli :

livello A1 -> ex biennio formativo,

livello A2 -> ex biennio d'indirizzo,

livello A3 -> ex quinto anno

( versione PDF )

 

 

Un percorso più rogoroso (e quindi più avanzato) sulla  funzione esponenziale

Argomenti di matematica generale

Dalle progressioni geometriche alla funzione esponenziale

Il numero e

... e altre spigolature

 funzione_exp.html

 

gioca con le isometrie di base

 

 

derivate e antiderivate (primitive)

 

 

matematica di base

 

approssimazione dell'esponenziale immaginario exp(it) nell'intervallo t ∈ [0,1]

( premi Step per aumentare il numero naturale n e Clear per ripristinarlo a 1 )

approssimazione di exp(at), con a complesso, nell'intervallo t ∈ [0,1]

( fissa a e premi Step per aumentare il numero naturale n e Clear per ripristinarlo a 1 )

ancóra sull'esponenziale naturale

clicca sul pulsante :

prendiamo un punto a = ( ax , ay ) = ( h , k ) "vicino" al punto (0,1)

suddividiamo l'asse delle ascisse con i punti n h (con n interi)

indichiamo con Zh l'insieme dei numeri della suddetta suddivisione

ipotizziamo che una funzione f definita su Zh sia tale che :

f( 0 ) = 1 ; f( h ) = k ; f( x+h ) = f( x ) k , per ogni x in Zh

a parole: f passa per (0,1) e (h,k) e all'incrementare la x di h f(x) viene moltiplicata per k

ne deriva che f( n h ) = k n . Posto x = n h , si ha f( x ) = k x / h .

Poniamo 1 + p = ay = k : si ha f( x ) = [ (1 + p) 1 / h ] x

quindi f è l'esponenziale di base (1+p) 1 / h .

Se avviciniamo il punto a al punto (0,1) l'esponenziale f varia secondo il tipo di avvicinamento di a al punto (0,1) e "intorno" a (0,1)   f   diventa "instabile" .

Proviamo a far tendere a al punto (0,1) con a sulla retta y = 1+x

Ciò significa che ay = 1 + ax , ossia k = 1 + h .

in tal caso si ha f( x ) = [ (1 + h) 1 / h ] x e ...

... se prendiamo h = 1/n otteniamo (1 + h) 1/h = (1 + 1/n) n

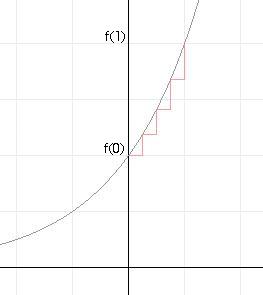
Quando h tende a 0, a, vincolato alla retta, tende a (0,1) ...

... e f( x ) tende a e x ; il segmento verticale in figura è (1,0)_(1,e)

Cosa accade se l'avvicinamento è effettuato sulla retta y=1+m x ?

Che cos'è un algoritmo Informazioni, dati e strutture dati Rappresentazione degli algoritmi Alcuni esempi di algoritmi Imparare a programmare Introduzione a Javascript

I t e r a z i o n e    " p e r  v e r o "      ( ciclo   " w h i l e "  )  Nell'algoritmo per l'implementazione del costrutto VECTOR abbiamo visto che uno stesso gruppo  I  di istruzioni viene ripetuto ciclicamente per tutto il tempo in cui una condizione  C  viene trovata vera. Questo ciclo è detto "iterazione per vero" oppure "iterazione con uscita per falso". Il diagramma è : : : _|_ / falso *->-/ C --->* | / | | _ _/ | | vero| | | __|__ | | | | | *-<-| I | | |_____| | | *<------* | : : un altro possibile diagramma, perfettamente equivalente, è : : : |<----------* _|_ | / vero | / C --->* | / | | _ _/ __|__ ^ | | || falso | I || | |_____|| : | | : *->-*   La versione testuale di tale ciclo iterativo è : mentre  C  esegui  I (   while   C  do  I   )   La naturale definizione sarebbe teoricamente:    (1) mentre(C,I) := IF( C , mentre(C,I) , "fine ciclo" ) Però Derive quando valuta una funzione definita dall'utente per prima cosa cerca di valutarne gli argomenti (ossia gli input; in questo caso C e I) e solo dopo applica la definizione della funzione; pertanto la valutazione della espressione mentre(C,I) di sopra verrebbe effettuata con i valori trovati per C e per I la prima volta che tale valutazione è eseguita e, se C risulta vera si entra in un loop senza uscita, mentre se C risulta falsa si accede subito alla stringa "fine ciclo". Esiste però un operatore (operatore "apice", con simbolo ' ) , detto operatore di "citazione" ("quote operator") o di "differimento di valutazione", che anteposto a una espressione produce un'espressione "citante" la cui valutazione è l'espressione "citata". Ad esempio se, dopo aver posto x := 4 , valutiamo (col pulsante "=") x+2 , il risutato della valutazione è 6 , mentre se valutiamo '(x+2) oppure 'x + 2 il risultato è x+2, in quanto nel primo caso rimane inalterata (quindi non valutata) l'intera espressione (x+2) , mentre nel secondo rimane non valutata la variabile x (che è un tipo elementare, o "atomico", di espressione). Nelle espressioni funzionali con argomenti "apiciati" (ossia she sono espressioni sottoposte all'operatore  ' ) Derive non effettua la preventiva valutazione di tali argomenti. Perciò potremmo usare nell'espressione mentre(C,I) espressioni con apici; ad esempio: C := '(x<=10) e I := '[v := APPEND(v, [x^2]); x := x + 1] e in tal caso Derive non valutando C e I produce internamente, tramite la definizione di sopra      (2)     IF( '(x<=10) , mentre('(x<=10),'[v := APPEND(v, [x^2]); x := x + 1]) , "fine ciclo" ) poi semplifica ciò che può valutare e produce:     (2bis)   IF( x<=10 , mentre(x<=10,[v := APPEND(v, [x^2]); x := x + 1]) , "fine ciclo" ) quindi non effettua alcun ciclo; e, del resto, se continuassimo con la valutazione della espressione (2) ricadremmo nel loop senza termine (dal momento che adesso gli apici non ci sono più). Esiste però un modo per costringere Derive a valutare direttamente un'espressione con apice. Uno possibile e definire le seguenti funzioni :      testa(L) := L SUB 1      valuta(E) := testa([E]) La prima prende il primo elemento (detto "la testa") di una lista, ad esempio:                            testa([1,2,3,4])   viene valutato :    1 La seconda prende una espressione E, la valuta, usa il risultato r per costruire una lista [r] costituita solo da tale risultato e poi valuta testa([r]), per la quale cosa valuta r nell'espressione [r] per poi applicare la definizione della funzione testa. Pertanto se partiamo dall'espressione (un numero è una particolare espressione, costante) 5 l'espressione valuta(5) viene valutata seguendo i seguenti passi : - si valuta il 5 e il risultato è ... 5 ; - si segue la definizione della funzione "valuta" e quindi si ottiene testa([5]) ; - si valuta l'input ("argomento") presente nell'espressione testa([5]) , ossia [5], e si ottiene testa([5]) ; - si applica la definizione della funzione "testa" pervenendo a [5] SUB 1, ossia 5. Proviamo, dopo aver gia definito x:=4 come già fatto, a valutare l'espressione valuta(x) seguendo gli stessi passi di sopra : - si valuta x e il risultato è 4 ; - si segue la definizione della funzione "valuta" e quindi si ottiene testa([4]) ; - si valuta l'input ("argomento") presente nell'espressione testa([4]) , ossia [4], e si ottiene testa([4]) ; - si applica la definizione della funzione "testa" pervenendo a [4] SUB 1, ossia 4. Proviamo adesso a valutare l'espressione valuta('x) : - non si valuta subito l'argomento 'x (in quanto è sotto la "protezione" dell'apice); - si segue la definizione della funzione "valuta" e quindi si ottiene testa(['x]) ; - si valuta l'input ("argomento") presente nell'espressione testa(['x]) , ossia ['x], e si ottiene testa([x]) ; - si applica la definizione della funzione "testa" pervenendo a [x] SUB 1, ossia x ; - l'ultima fase della valutazione di una funzione è la semplificazione, perciò l'espressione x viene valutata 4 . Come vediamo, così facendo partiamo da 'x e otteniamo non x ma il valore 4 della variabile x Altro esempio: valutiamo l'espressione (apiciata) '(x>0) : - non si valuta '(x>0) ; - si segue la definizione della funzione "valuta" e quindi si ottiene testa(['(x>0)]) ; - si valuta (semplifica) tale ultima espressione, ottenendo testa([x>0]) ; - si valuta testa([x>0]), quindi si provvede anzitutto a valutare [x>0] in [true] ; - si applica la definizione della funzione "testa" pervenendo a [true] SUB 1, ossia true. Un'altra osservazione sulla valutazione delle espressioni: se si è definita una funzione di due argomenti, ad esempio         potenza(base,esponente) := base ^ esponente e la si applica a più argomenti di quelli usati nella definizione, ad esempio :      (3)     potenza(3,2,x:=3) la definizione usa solo i primi argomenti che effettivamente le servono in base alla definizione pur però valutando tutti gli argomenti presenti in (3). Quindi, valutando la (3) si ottiene l'atteso 9 (ossia 3^2), ma ... x è diventato 3 (ricordiamoci che prima era stato definito come 4). Applichiamo quanto visto alla definizione della funzione "mentre". Definiamo:                     mentre(C,I) := IF( valuta(C) , mentre( C , I , valuta(I) ) , "fine ciclo" )   Poniamo preliminarmente le due definizioni ("assegnamenti")   x:=0    e   v:=[ ]   e supponiamo che   C  sia  '(x <= 10)   e che  I  sia  '[v := APPEND(v, [x^2]); x := x + 1]. In quanto apiciate, C e I vengono passate non valutate, ma poi IF determina la valutazione dell'espressione valuta(C), la quale risulta true per cui si procede a valutare l'espressione mentre(C,I,valuta(I)), il che comporta come effetto collaterale la valutazione dell'espressione valuta(I) ( cosa che fa eseguire I stessa ), prima di passare alla esecuzione di mentre(C,I), il che fa ricominciare il tutto, ma dopo la valutazione di I  ( che ha modificato il valore della variabile x )   In definitiva: digitiamo in Derive (riga di editing): testa(L) := L SUB 1 valuta(E) := testa([E]) mentre(C,I) := IF(valuta(C),mentre(C,I,valuta(I)),"fine ciclo") Verifichiamo il funzionamento digitando, e poi valutando : [v := []; x := 0; mentre('x <= 10, '[v := APPEND(v, [x^2]); x := x + 1]); v; x] l'output sarà : ¦ [] ¦ ¦ ¦ ¦ 0 ¦ ¦ ¦ ¦ fine ciclo ¦ ¦ ¦ ¦ [0, 1, 4, 9, 16, 25, 36, 49, 64, 81, 100] ¦ ¦ ¦ ¦ 11 ¦

inseriamo in Derive le seguenti espressioni

espressione(x) := x^2   inizio := 0   fine := 10   passo := 2   lista := VECTOR(espressione(x) , x , inizio , fine , passo)   lista

la valutazione della variabile  "lista"  tramite il pulsante  "="  da' : [0, 4, 16, 36, 64, 100]

lo "schema di flusso" del processo effettuato dall'espressione  VECTOR(espressione(x) , x , inizio , fine , passo)  e' il seguente : v := [ ] x := inizio (1)       condizione :      x <= fine    ? sì no v := append(v,[espressione(x)]) l'output del processo e' :     v x  :=  x + passo torna a (1)

Un modo per realizzare ("implementare") tale processo (algoritmo) in DERIVE 5 e' digitare nella riga di editing (ovviamente dopo aver inserito le espressioni che definiscono espressione(x), inizio, fine e passo) l'espressione :  p := [v := [ ] ; x := inizio ; IF(x <= fine, [v := APPEND(v, [espressione(x)]) ; x := x + passo ; pSUB3SUB1], v)] (seleziona tutta l'espressione e dopo averla copiata con CTRL+C incollala con CTRL+V nella riga di editing di DERIVE, quindi premi INVIO) con tale espressione selezionata, valutarla tramite il pulsante "=" ;  si otterra' la "traccia" dell'algoritmo.

Un altro modo, piu' elegante e veloce, per implementare l'algoritmo e' definire la seguente funzione ciclo(v,x) :    ciclo(v, x)  :=  IF(  x <= fine  ,  ciclo( APPEND(v, [espressione(x)]) ,  x + passo )  ,  v ) e quindi valutare con il pulsante "=" l'espressione : ciclo( [ ] , inizio ) Prova a inserire tali due espressioni nella riga di editing di DERIVE e a valutare la seconda con "=". Questo secondo procedimento non richiede di dare un nome all'intero programma (sopra era chiamato p) per indirizzarne una parte a cui ritornare ciclicamente, ma isola la parte del processo che si ripete ciclicamente e la definisce come funzione degli ingressi ("input") che tale ciclo deve elaborare, ingressi che vengono automaticamente modificati dalla funzione stessa nel suo "corpo" senza riassegnamento di variabili. Infine tale funzione viene applicata agli input di partenza che sono la lista vuota [ ] e il numero contenuto nella variabile "inizio" .

facciamo il punto sulle applet PGC finora viste :

ciclotomia e radici dell'unità

triangolo rettangolo e circonferenza circoscritta

rotazioni intorno all'origine

prodotto di numeri complessi

somma di angoli

esponenziale naturale di un numero immaginario

funzioni a scala

come render giustizia ( "orthòs" = "giusto" -> ortogonale ) all'obliquità

parabola e moltiplicazione grafica

parabole, traslazioni, equazioni quadratiche

funzioni lineari e progressioni aritmetiche

funzioni esponenziali e progressioni geometriche

incrementi di una funzione

funzioni elementari

mettere la freccia ad un vettore

esponenziale naturale e numero di Nepero

facciamo la TAC alla moltiplicazione !

interpolazione e combinazioni lineari

vettori e traslazioni "versus" flettori e rotoomotetie

le 8 ( ma in fondo solo 2 ) isometrie fondamentali del piano

 

matematica con DERIVE

 

usa o scarica l'applet PGC ( plane graphic calculator = calcolatrice grafica nel piano )

decomprimi il file zip in una cartella e avvia uno dei due file in formato HTML :

PGC.html oppure index.html

 

Matematica per il biennio delle scuole superiori (con Derive e Cabri)

Seleziona e copia il testo sottostante compreso fra le righe di asterischi, quindi apri il blocco note (notepad) e incolla quanto copiato; salvalo scegliendo l'opzione "salva come: tutti i file", dandogli il nome esercitazione.mth, quindi aprilo con DERIVE 5 (o DERIVE 6). Buon lavoro ! ********************************************************************************* " Primo approccio alla grafica con DERIVE 5 " punto(a,b):=[a,b] "clicca sul pulsante ''finestra grafica 2D'' e poi scegli: finestra > affianc~ a (o disponi) verticalmente " "dopo aver selezionato la finestra grafica, scegli: opzioni > semplifica prim~ a di tracciare il grafico" "seleziona l'espressione di qui sotto, poi seleziona la finestra grafica, qui~ ndi clicca sul pulsante ''Traccia il grafico dell'espressione'' " punto(2,3) "seleziona l'espressione di qui sotto, poi seleziona la finestra grafica, qui~ ndi clicca sul pulsante ''Traccia il grafico dell'espressione'' " punto(3,2) " cancella la figura con la combinazione di tasti Ctrl+D " fig(a,b):=[punto(a,b),punto(-a,b),punto(a,-b),punto(-a,-b)] "seleziona l'espressione di qui sotto, poi clicca sul pulsante ''='' osserva ~ come DERIVE sviluppa l'espressione, quindi ritorna su fino alla prossima istr~ uzione " fig(a,b) "seleziona l'espressione di qui sotto, poi seleziona la finestra grafica, qui~ ndi clicca sul pulsante ''Traccia il grafico dell'espressione'' " fig(3,2) " cancella la figura con la combinazione di tasti Ctrl+D " figsim(a,b):=APPEND(fig(a,b),fig(b,a)) figsim(a,b) ;Sempl(#17) [[a,b],[-a,b],[a,-b],[-a,-b],[b,a],[-b,a],[b,-a],[-b,-a]] "seleziona l'espressione di qui sotto, poi seleziona la finestra grafica, qui~ ndi clicca sul pulsante ''Traccia il grafico dell'espressione'' " figsim(2,3) " cancella la figura con la combinazione di tasti Ctrl+D " punto_su_arco(t):=punto(COS(t),SIN(t)) "seleziona una dopo l'altra le espressioni di qui sotto e ogni volta selezion~ a la finestra grafica, quindi clicca sul pulsante ''Traccia il grafico dell'e~ spressione'' " punto_su_arco(1) punto_su_arco(1/2) punto_su_arco(1/3) punto_su_arco(2/3) punto_su_arco(1/4) punto_su_arco(3/4) VECTOR(punto_su_arco(t),t,0,1,0.1) VECTOR(punto_su_arco(t),t,0,1,0.01) VECTOR(punto_su_arco(t),t,0,pi,0.01) " cancella la figura con la combinazione di tasti Ctrl+D " "seleziona l'espressione di qui sotto, poi seleziona la finestra grafica, qui~ ndi clicca sul pulsante ''Traccia il grafico dell'espressione'' " VECTOR(punto_su_arco(t),t,0,pi,pi/15) " cancella la figura con la combinazione di tasti Ctrl+D " "seleziona l'espressione di qui sotto, poi seleziona la finestra grafica, qui~ ndi clicca sul pulsante ''Traccia il grafico dell'espressione'' " VECTOR(punto_su_arco(t),t,0,2*pi,pi/15) " cancella la figura con la combinazione di tasti Ctrl+D " stella:=VECTOR(r*punto_su_arco(t),t,0,2*pi,pi/15) "seleziona l'espressione di qui sotto, poi seleziona la finestra grafica, qui~ ndi clicca sul pulsante ''Traccia il grafico dell'espressione'' ; si aprira'~ una finestra che chiede i valori minimo e massimo; imposta rispettivamente ~ a 0 e a 1 tali valori e spunta la voce ''applica i parametri anche agli altri~ grafici''" stella " cancella la figura con la combinazione di tasti Ctrl+D " stelle(a,b):=VECTOR(VECTOR(r*punto_su_arco(t)+p,t,0,2*pi,pi/15),p,figsim(a,b)~ ) "seleziona l'espressione di qui sotto, poi seleziona la finestra grafica, qui~ ndi clicca sul pulsante ''Traccia il grafico dell'espressione'' ; si aprira'~ una finestra che chiede i valori minimo e massimo; tali valori sono gia' i~ mpostati rispettivamente a 0 e a 1 ed e' gia' spuntata la voce ''applica i pa~ rametri anche agli altri grafici''; quindi clicca solo su OK" stelle(2,3) " cancella la figura con la combinazione di tasti Ctrl+D " fuochi(a,b,n):=VECTOR(stelle(a*s,b*s),s,0,1,1/n) " rappresenta, come prima indicato, nella finestra grafica l'espressione segu~ ente : " fuochi(6,3,3) " clicca sul pulsante ''riduci'' " " clicca nuovamente sul pulsante ''riduci'' " " clicca sul pulsante ''ingrandisci'' " " clicca nuovamente sul pulsante ''ingrandisci'' " " cancella la figura con la combinazione di tasti Ctrl+D " fascio(a,b):=APPEND(figsim(a,b),VECTOR(p SUB 2/p SUB 1*x,p,figsim(a,b))) " rappresenta nella finestra grafica l'espressione seguente : " fascio(3,2) " cancella la figura con la combinazione di tasti Ctrl+D " ott(a,b):=[[a,b],[b,a],[-b,a],[-a,b],[-a,-b],[-b,-a],[b,-a],[a,-b],[a,b]] "dopo aver selezionato la finestra grafica, scegli: opzioni > visualizzazione~ > punti e imposta su si' l'opzione ''collega'' " " rappresenta nella finestra grafica l'espressione seguente : " ott(3,2) " cancella la figura con la combinazione di tasti Ctrl+D " " rappresenta nella finestra grafica l'espressione seguente : " ott(2,3) " cancella la figura con la combinazione di tasti Ctrl+D " ottagono(a,b):=IF(a>=b,ott(a,b),ott(b,a)) " rappresenta nella finestra grafica l'espressione seguente : " ottagono(2,3) " cancella la figura con la combinazione di tasti Ctrl+D " le_8_isometrie(a,b):={ottagono(a,b),fascio(a,b)} " rappresenta nella finestra grafica l'espressione seguente : " le_8_isometrie(2,3) " fine dell'esercitazione " *********************************************************************************

 

Rappresentazione della conoscenza e tecnologie Web

 

 

rappresentazione della conoscenza

 

	Maria Luisa Dalla Chiara Roberto Giuntini Francesco Paoli Sperimentare la logica Editore: Liguori (NA) ISBN: 88-207-3684-5 ed.: 2004 pp.: 180

Sperimentare la logica è un manuale introduttivo di logica pensato per l’utilizzo nella didattica universitaria triennale ed esplicitamente indirizzato non solo agli studenti di Filosofia, ma anche agli studenti di Scienze e Tecniche Psicologiche, Scienze dell’Educazione, Scienze della Comunicazione o Scienze della Formazione Primaria. La scelta dell’impostazione e dei contenuti del manuale è stata dettata da un’attenta considerazione dei mutamenti intervenuti nell’insegnamento della logica con l’entrata in vigore della legge di riforma universitaria. In quest’ottica si è privilegiato, da un lato, un approccio alla logica di tipo informale, semantico, e, dall’altro, ci si è impegnati a evitare il più possibile le astrazioni filosofico-matematiche a vantaggio delle esemplificazioni concrete, dell’aderenza al linguaggio ordinario e al ragionamento quotidiano, dell’esplorazione di possibili intersezioni con la psicologia, la didattica, le scienze cognitive, la pragmatica della comunicazione.

 

XML :  un (meta)linguaggio per la rete e per l'organizzazione delle informazioni e delle conoscenze

Recupero programma di primo livello

L’insieme N dei numeri naturali e operazioni di addizione, moltiplicazione ed elevamento a potenza. Commutatività, associatività, elemento neutro, distributività. Rappresentazione cartesiana dei numeri naturali. L’insieme Z dei numeri interi relativi e il piano a coordinate intere (“griglia”). Addizione e moltiplicazione di numeri relativi. Interpretazione della moltiplicazione sul piano a coordinate intere e il concetto di proporzionalità diretta. Addizione di punti del piano a coordinate intere (tramite le componenti orizzontale e verticale). Minimo comune multiplo e massimo comun divisore, con applicazioni a problemi pratici di composizione e scomposizione di figure rettangolari. Elevamento a potenza con esponente intero negativo. L’insieme Q dei numeri razionali e le operazioni di addizione e moltiplicazione. Il piano a coordinate razionali e l’interpretazione grafica dell’addizione e della molltiplicazione. Densità dell’insieme Q. Proprietà invariantiva delle frazioni. Concetto di “rapporto”. Espressione decimale di una frazione. Numeri periodici. Trasformazione da frazione a decimale e viceversa. Potenze a esponente intero di numeri razionali. Proprietà dell’elevamento a potenza. Divisione in Q. Calcolo con espressioni intere e frazionarie. Il piano cartesiano come ambiente algebrico dotato di un’operazione di addizione e la regola del parallelogramma. Le due unità reale (1) e immaginaria (i) : espressione di punti come somme di multipli di 1 e i. Monomi: grado, coefficienti e similitudine. Monomi, addizione e generazione dei polinomi come somma di monomi. Monomi e operazione di moltiplicazione. Monomi razionali e operazione di divisione. Operazioni su espressioni letterali. Rappresentazioni di espressioni di primo grado contenenti una sola variabile (x) nel piano cartesiano.

 

***

 

informatica (laboratorio)

 

Introduzione alla gestione dei files nel sistema operativo Windows. I software di Computer Aided Design (disegno Assistito da Computer) e il programma Cabri-Géomètre. Gli strumenti Punto, Retta, Segmento, Retta Perpendicolare, Retta Parallela. Lo strumento Circonferenza. Intersezine di oggetti. Lo strumento “Assi Cartesiani” in Cabri. Ascisse e ordinate. Lo strumento Macro e la determinazione di un sistema cartesiano ortogonale con singola unità di misura sui due assi, in dipendenza di soli due punti (origine e unità). Lo strumento Griglia su un sistema di assi cartesiani. Lo strumento Coordinate (di un punto rspetto a un sistema di assi cartesiani). Punti su un oggetto (ossia vincolati). Lo strumento Calcolatrice e il Trasporto di Misura per riportare un numero su un asse. Grafici cartesiani di leggi espresse come espressioni con variabile indipendente x sull’asse delle ascisse. Descrizione testuale di una costruzione tramite una tabella con due colonne (passo e azione/costruzione). Simmetrie e poligoni con Cabri-Géomètre. L’esigenza di rappresentare un documento e in generale informazioni strutturate tramite testo. Il blocco note di Windows e la strutturazione tramite Tags. Struttura generale di un documento con codifica HTML. Tags (o marcatori) e loro attributi. Strutturazione del tipo e dell’aspetto di un carattere tramite tags. Creazione di pulsanti e caselle di testo e loro gestione mediante istruzioni subordinate ad eventi (simulazione di una elementarissima calcolatrice che però permette l’uso di variabili). Creazione e formattazione di collegamenti tramite il tag di ancoraggio e i suoi attributi. Rappresentazione ad albero di un documento HTML. Cenni sulla creazione di tabelle in HTML. Struttura tabulare di un foglio di Excel. I valori di verità VERO e FALSO e le operazioni logiche AND (E) e OR (O) e il loro uso in Excel per “filtrare” elementi dati in base a loro proprietà; applicazione a problemi concreti. Rappresentazione ad albero di un’epressione con AND e OR.

Recupero programma di terzo livello

 

Concetto di operazione su un insieme, intesa come processo che porta da uno o più input ad un output. Operazioni ad un input (operatori) e a due input (operazione in senso stretto) e diagrammi rappresentativi input-processo-output. Distinzione fra sintassi (gestione delle espressioni simboliche) e semantica (interpretazione – o significato – delle espressioni simboliche) di una teoria matematica. Prima formalizzazione della struttura matematica dello spazio tramite un insieme S dotato di un elemento 0 (origine o zero) e di una operazione (addizione) commutativa, associativa, con elemento neutro 0 e simmetrizzabile (nozione di “opposto”), interpretata graficamente tramite la “regola del parallelogramma”. Unicità dell’opposto e operatore “-“ di opposizione; definizione dell’operazione di sottrazione tramite la regola definitoria x-y := x+(-y), con diagramma di tale definizione. Interpretazione geometrica dell’opposizione (simmetria rispetto a 0) e della sottrazione (seconda diagonale del parallelogramma). Interpretazione degli elementi di S oltre che come punti anche come “vettori”. Concetto di funzione come trasformazione o passaggio da un dato a un risultato e interpretazione dell’addizione (con un addendo fissato) come traslazione. Aggiunta alla struttura (S, 0, +) di un sottoinsieme R⁺ (insieme dei numeri reali positivi) di S, interpretato graficamente come una semiretta. Simbolo di appartenenza e definizione della relazione di ordine “<” (“minore”) tramite la regola definitoria ( x := ( y-x Î R⁺) . Definizione della relazione di ordine “>” (“maggiore”), inversa della precedente. Simbolo di disgiunzione OR e introduzione delle altre due relazioni di ordine, “minore o uguale” e “maggiore o uguale”.

Simbolo di congiunzione AND e introduzione delle proprietà di base di R⁺ basate sulla relazione “minore”: chiusura rispetto all’operazione di addizione, densità, tricotomia, continuità (quest’ultima per cenni intuitivi). Semiretta dei numeri reali negativi. Simbolo di unione e definizione dell’asse reale R come unione delle semirette positiva e negativa con l’aggiunta di 0. Introduzione di un altro elemento privilegiato oltre allo zero: l’unità (1). Numeri naturali (N), interi relativi (Z). Multipli di un elemento di S, con coefficienti in N e più in generale in Z. Frazionabilità di 1, intesa come divisibilità di 1 per un qualunque numero naturale non nullo e simbolo di divisione “/”. Impossibilità della divisione 1/0. Definizione delle frazioni tramite la regola m/n := m(1/n). Insieme Q dei numeri razionali. Nozione di “inverso”, contrapposta a quella di “opposto”. Esistenza di altri numeri in R oltre agli elementi di Q (ossia di numeri non razionali, ovvero “irrazionali”). Moltiplicazione di un elemento qualunque (moltiplicando) di S con coefficiente (moltiplicatore) razionale, con interpretazione geometrica. Cenno alla generalizzazione del multiplo al caso di coefficiente reale qualunque. Genesi, basata su moltiplicazione e addizione (quest’ultima per traslare), dei concetti di segmento (moltiplicatore compreso fra 0 e 1), semiretta (moltiplicatore positivo o non negativo), retta (moltiplicatore arbitrario). Formula a + (b-a) t come generatrice di tali figure al variare del parametro t. Combinazioni lineari di due elementi di S. Aggiunta di un terzo elemento privilegiato in S, l’unità immaginaria i. Interpretazione grafica “ortonormale” (ossia ortogonale e monometrica) e “antioraria” della terna (0, 1, i). L’insieme dei numeri complessi C, generato dalle combinazioni lineari di 1 (unità reale) e i (unità immaginaria). Simmetria rispetto all’asse reale e numeri complessi coniugati. Opposizione e simmetria centrale (rispetto all’origine). Simmetria rispetto all’asse immaginario. Parte reale e operatore Re( ) ; coefficiente della parte immaginaria e operatore Im( ) . Scambio di Re(z) con Im(z) e simmetria rispetto alla bisettrice di 1° e 3° quadrante. Ortogonali antiorario e orario di un numero complesso. Uso privilegiato dell’operatore ort( ) che fornisce l’ortogonale antiorario. Moltiplicazione di due numeri complessi basata sul cambiamento di riferimento da (0,1,i) a (0,z,ort(z)), dove z è il moltiplicando. Espressione algebrica della moltiplicazione e relazione fondamentale frale due unità: i² = -1. Interpretazione della moltiplicazione (con moltiplicando fisso z, ossia “moltiplicazione per z”) come rotodilatazione che trasforma 1 in z. Condizione affinché una rotodilatazione per z sia una rotazione: il coniugato di z viene trasformato in 1 dalla moltiplicazione per z ; numeri complessi unitari (lunghi come l’unità). Modulo di un numero complesso e sua relazione pitagorica con le componenti del numero stesso. Esempi di uso delle operazioni di addizione e moltiplicazione in C (e del modulo) per la grafica computerizzata.

Recupero programma di quarto livello

 

Richiamo del concetto di funzione: variabile indipendente, processo (la funzione stessa) e variabile dipendente. Funzioni date con un’equazione del tipo y=f(x), soddisfatta da tutte e sole le coppie (x,y) che la funzione associa tramite la formula data. Funzioni definite su tutto l’insieme dei numeri reali o su un suo intervallo. Funzioni lineari: richiamo intuitivo in base alla formula y = ax + b, con significato dei parametri a e b. Concetto di incremento di una funzione nel passaggio da un valore iniziale del suo argomento ad un valore incrementato. Rappresentazione cartesiana dell’incremento come lunghezza del cateto verticale del triangolo rettangolo con un vertice nel punto del grafico di ascissa iniziale x e l’ipotenusa secante il grafico della funzione nel predetto punto e in quello di ascissa incrementata. Uso della variabile incrementale, ad esempio di Dx come variabile incrementale associata alla variabile indipendente x. Estensione dell’operatore D alle espressioni funzionali f(x) e quindi alle variabili dipendenti. Variazione (o crescita) assoluta di una funzione in un intervallo e velocità media di crescita (ossia crescita relativa rapportata alla variazione della variabile indipendente); rapporto incrementale e suo possibile assestamento intorno a un valore limite quando l’incremento della variabile indipendente tende a zero (velocità istantanea di crescita della funzione in corrispondenza all’ascissa data, ovvero derivata della funzione in corrispondenza di tale ascissa). Interpretazione geometrica del rapporto incrementale come pendenza dell’ipotenusa del triangolo rettangolo associato alla funzione nel punto dato e per l’incremento dato. Interpretazione del limite che fornisce la derivata (se esiste) come pendenza della retta tangente al grafico, sussistente come retta anche quando l’ipotenusa che la definisce scompare. Funzioni lineari ottenute in base alla proprietà di associare incrementi uguali delle ordinate ad incrementi uguali delle ascisse. Deduzione della formula già nota per le funzioni di primo grado nella forma f(x)=ax+b con a=f(1)-f(0) e b=f(0) (facendo uso del metodo di progressione aritmetica).

Concetto di rapporto (o “inceremento per rapporto”) di una funzione : f(x+Dx) / f(x) . Funzioni che associano a incrementi uguali delle ascisse rapporti uguali delle ordinate. L’esempio delle lunghezze di corde producenti note musicali. Enucleazione delle somiglianze formali con il caso delle funzioni lineari, sostituendo però alla differenza dei valori il rapporto degli stessi. Deduzione, col metodo di progressione geometrica, della formula f(x) = (a^x)b, simile nella struttura ad ax+b ma con un grado di astrazione operazionale in più (l’addizione diventa moltiplicazione e la moltiplicazione diventa elevamento a potenza). Definizione di potenza ad esponente frazionario (positivo o negativo) proprio per realizzare la validità della precedente formula per ogni ascissa razionale x. Proprietà delle funzioni esponenziali y=a^x (somma e differenza degli argomenti e potenza di potenza). Introduzione della funzione esponenziale naturale partendo dal modello di capitalizzazione composta su periodi di uguale lunghezza p e facendo poi tendere tale lunghezza a zero per avere una capitalizzazione continua (ovvero “istante per istante”). Numero di Nepero come limite della successione (1+1/n)ⁿ e come base della funzione esponenziale naturale introdotta.

Simmetrie rispetto agli assi coordinati e relazione grafica fra le funzioni f(x) , f(-x) , -f(x) e –f(-x). Scambio delle coordinate x e y nella formula y=f(x) e grafici simmetrici rispetto alla bisettrice principale (del primo e terzo quadrante: y=x ). Introduzione algebrica e geometrica (con la predetta simmetria di inversione) delle funzioni logaritmiche a partire dalle funzioni esponenziali. Concetto di base di una funzione logaritmica e valori accettabili per tale base, oltre che confronto fra i casi in cui essa è maggiore di 1 con quelli in cui essa è inferiore ad 1. Valori accettabili per la x nell’espressione log_a x . Proprietà di base dei logaritmi: logaritmo di prodotto e quoziente, logaritmo di una potenza, espressione di una logaritmo tramite logaritmi in un’altra base data. Velocità di crescita istantanea (derivata) della funzione logaritmica in base a e relazione di reciprocità (motivata geometricamente) con la corrispondente velocità istantanea della funzione esponenziale associata.

integrali per l'esame di maturità

Ricetta semi-etimologica per una religione *** Legacci vari. Un re. Una ragione o una regione. Una ligia legione. E dei relé.

grafici in HTML

(per internet explorer 5+)

vedi anche questo file (che permette l'esportazione del grafico)

rebus
( monoverbo onomastico : 3,1,1,1,3,1 = 10 )
 
Le tre " i "

un...

un singolare anagramma

società di mercato ...

... cometa di sorcietà

Esercitazione con  esplorHTML

Prova le seguenti stringhe di codice html (copia e incolla nell'area di esplorHTML la stringa posta fra le sequenze di asterischi )

1) valutatore con doppio clic sull'area di output : ( l'evento che attiva la valutazione sarà il doppio clic sulla seconda casella ) ******************************************************************** <input id=input type=text value=input> = <input id=output type=text value=output   ondblclick="output.value=eval(input.value)"> ********************************************************************

1bis) come sopra con una piccola differenza ( quale? ) : ******************************************************************** <input id=input type=text value=""> = <input id=output type=text value="" ondblclick="output.value=eval(input.value)"> ********************************************************************

2) valutatore con singolo clic sul pulsante " = " ( l'evento che attiva la valutazione sarà il clic sul pulsante "=" ) ******************************************************************** <input id=input type=text value="" > <input type=button value="=" onclick="output.value=eval(input.value)" > <input id=output type=text value="" > ********************************************************************

con le caselle ottenute da 1 e da 2 valuta le seguenti espressioni: (digita l'input nella prima casella e valutane il contenuto con l'evento appropriato) ( NON digitare il numero con parentesi che sta all'inizio: è solo un indice di elenco ) 1) a=3 ; b=6 ; a*b 2) a+b 3) a=5 ; a*b 4) a=4 5) a=null 6) a+b 7) [a,b] 8) a=5 ; [a,b,b,a] 9) a=true 10) a+4 11) a=false 12) a+4

3) trasformatore in maiuscolo ******************************************************************** <input id=input type=text value="" onkeyup="output.value=input.value.toUpperCase()" > --> <input id=output type=text value="" > ********************************************************************

4) invertitore di stringhe ******************************************************************** <input id=input type=text value="" onkeyup="output.value=input.value.charAt(input.value.length-1)+ output.value" > --> <input id=output type=text value="" > ********************************************************************

le otto is...

 

le otto isometrie fondamentali del piano

una 'cassetta' di st...

una 'cassetta' di strumenti web

<	>	esplorHTML
=	"
È	Ç	unicoder
Ì	É
e	i	dim_imag
d	o

il concetto di funzione

&n...

     clicca qui per esercitarti con Cabri

traslazion...

traslazioni , rotodilatazioni ...
... e loro traiettorie ( clicca sui pulsanti )
( muovi b e z = a , c , d nelle figure )
traslazione di "vettore" b Tb : z --> Tb ( z ) := z + b
rotodilatazione di "flettore" b Rb : z --> Rb ( z ) := z · b

ricorsione e iterazi...

ricorsione e iterazione in un contesto funzionale  ( MathView )

l o g a ...

l o g a r i t m i   :       proprietà  ( regole di calcolo )   fondamentali
Partiamo da:     y = ax
y = expa ( x )        ( definizione di exp )	x = loga ( y )       ( definizione di log )
y' = expa ( x' )	x' = loga ( y' )
y · y'  =  expa ( x ) · expa ( x' )	x + x'  =  loga ( y ) + loga ( y' )
a x + x'   =  a x  ·  a x'     ( proprietà della somma degli esponenti )
y · y'  = ax · ax' = ax+x' = expa ( x + x' )	=>             x + x'  =   loga ( y · y' )
expa ( x + x' ) = expa ( x ) · expa ( x' )	loga ( y ) + loga ( y' ) =  loga ( y · y' )
(1) regola del logaritmo di un prodotto :      loga ( y · y' ) = loga ( y ) + loga ( y' )
a x  x'   = ( a x ) x'          ( proprietà del prodotto degli esponenti )
y = expa ( x )	x = loga ( y )
yc = ( expa(x) )c = ( ax )c = ax·c = expa(x·c)	=>                x c   =  loga ( y c )
expa ( x · c ) = ( expa (x) ) c	loga (y) · c  = loga ( y c )
(2) regola del logaritmo di una potenza :           loga ( y c ) = c · loga (y)
c = -1	b = y c         ( =>  c = logy (b)  )
loga ( y -1 ) = (-1) · loga (y)	loga (y c) = loga (y) · c = loga (y) · logy (b)
loga ( 1 / y ) = - loga ( y )	loga ( b ) = loga (y) · logy (b)
loga( z / y )=loga(z · 1/y)=loga(z) - loga(y)	logy ( b ) = loga ( b ) /  loga ( y )
^  regola del logaritmo di un quoziente	^   regola del cambiamento di base

classe 4^S

 

1) Sia f(x) = -1/x a) determinare la crescita di f nel passaggio della variabile indipendente da x a x+Dx , ossia Df(x) b) determinare la velocità di crescita di f nel passaggio della variabile indipendente da x a x+Dx c) determinare la velocità di crescita di f istantanea nel valore x della variabile indipendente

2) Supponendo che una funzione f abbia la seguente proprietà:           f( x + Dx ) - f( x ) = f( x' + Dx ) - f(x')     per ogni scelta di x, x', Dx a) provare che: f(x+1) - f(x) = f(1) - f(0) per ogni scelta di x b) provare che: f(x + 1/4) - f(x) = f(1/4) - f(0)  per ogni scelta di x c) provare che: 4(f(1/4)-f(0))=f(1)-f(0)          e quindi f(1/4) - f(0) = (f(1) - f(0))/4 d) provare che:  f(3/4)=f0)+(3/4)(f(1)-f(0)) . e) Qual è la espressione generale di f(m/n) se f(0)=3 e f(1)=5 ? f) Disegnare il grafico di f nel caso in cui si abbia f(0)=3 e f(1)=5 .

3) Supponendo che una funzione f abbia la seguente proprietà:       f( x + Dx )/f( x )=f(x'+ Dx)/f(x') per ogni scelta di x, x', Dx a) provare che: f(x+1)/f(x) = f(1)/f(0) per ogni scelta di x b) provare che: f(x+1/4)/f(x)=f(1/4)/f(0) per ogni scelta di x c) provare che:    ( f(1/4) / f(0) )4 = f(1) / f(0)                e quindi f(1/4) / f(0) = ( f(1) / f(0) )1/4 d) provare che:    f ( 3/4 ) = f(0) ( f(1) / f(0) )3/4 . e) Qual è la espressione generale di f(m/n) se f(0)=2 e f(1)=4 ? f) Disegnare il grafico di f nel caso in cui si abbia f(0)=2 e f(1)=4.

4) Considerando un capitale pari a 1000 euro e prendendo come unità di tempo l'anno, qual è l'espressione matematica che dà il valore del capitale a fine anno nel caso si applichi un tasso di interesse pari a 0.01 (ossia 1%) e si ricapitalizzi a ogni fine mese (quindi 12 volte) ?

 

da oggi un nuovo blo...

da oggi un nuovo blog sulle novità editoriali riguardanti la matematica (e non solo)

                                      http://mathematedita.splinder.it

... il metodo ...

... il metodo piu' rigoroso e' anche il piu' semplice ed il piu' facile a capirsi. La ricerca del rigore ci conduce a scoprire ragionamenti sempre piu' semplici, e ci apre inoltre la strada a metodi piu' fecondi di quelli antichi, che erano meno rigorosi. David Hilbert

...